A busca por um algoritmo capaz de prever os números da Mega-Sena é tão antiga quanto a própria loteria. Com o avanço da Inteligência Artificial e do Big Data, muitos acreditam que estamos próximos de “decifrar o código”. No entanto, a ciência prova que o obstáculo não é a falta de tecnologia, mas as leis fundamentais do universo, a idéia aqui é mostrar a matemática por trás de tudo de uma forma simples.
Tenho estudado bastante alguns algoritmos preditivos e análiticos em minhas pós-gaduações em desenvolvimento de Inteligências Artificiais, e isso me chamou atenção porque nesta época do ano sempre aparece alguém com uma sequência mágica, um “jeito mágico” de calcular as sequências ou uma ideia mirabolante e precisando de alguém para “desenvolver”, neste artigo eu brinco um pouco com isso e busco mostrar a matemática por trás desse santo graal.
O Espaço Amostral e a Barreira Combinatória
A Mega-Sena é, fundamentalmente, um problema de Análise Combinatória clássica. Ao selecionarmos 6 dezenas em um universo de 60, estamos lidando com uma Combinação Simples (), onde a ordem dos números sorteados não importa para a definição do ganhador.
A Magnitude dos Números
O cálculo para determinar o número total de combinações possíveis é dado pela fórmula:
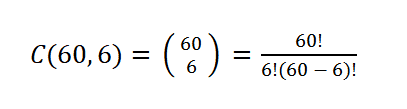
O resultado é de exatamente 50.063.860 de combinações distintas. Para o cérebro humano, acostumado a escalas lineares, é difícil processar o que esse volume representa. Para colocar em perspectiva:
- Esforço Temporal: Se você fosse capaz de preencher um bilhete por segundo, sem pausas para comer ou dormir, levaria aproximadamente 1 ano, 7 meses e 3 dias apenas para registrar todas as variações possíveis.
- A Probabilidade Decimal: A chance de acerto com uma aposta simples é de em , ou seja, ínfimos 0,00000199%.
A Isonomia das Combinações
A análise combinatória nos ensina um princípio vital e, muitas vezes, frustrante: não existem atalhos probabilísticos. No vácuo da matemática pura, a sequência “estética” 01-02-03-04-05-06 possui rigorosamente a mesma probabilidade de ser sorteada que qualquer outra combinação aparentemente “aleatória”.
O universo amostral é perfeitamente plano; cada uma das 50 milhões de combinações é um evento equiprovável. A sensação de que certos números são “melhores” que outros é um subproduto de vieses cognitivos, e não uma realidade matemática. A barreira combinatória é, portanto, o primeiro e mais sólido filtro que separa o desejo do apostador da realidade do prêmio.
A Independência Estatística e o “Viés de Memória”
O erro mais comum e persistente em análises preditivas de loteria é a má aplicação da Lei dos Grandes Números em amostras de tempo limitadas. Muitos analistas tentam forçar uma convergência estatística onde ela ainda não existe.
O Princípio dos Eventos Independentes
Em um sistema estocástico como o da Mega-Sena, cada sorteio é um experimento de Bernoulli isolado. Matematicamente, dizemos que o experimento possui correlação zero com o experimento .
Isso ocorre porque o mecanismo físico (o globo e as bolas) é “resetado” a cada concurso. Diferente de um jogo de cartas, onde a retirada de um Ás aumenta a chance de saírem cartas de outros valores (evento dependente), na loteria, as 60 bolas retornam ao globo com as mesmas propriedades físicas. A probabilidade de qualquer dezena ser extraída na primeira posição permanece estritamente:
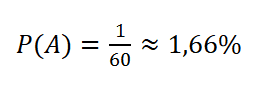
A Falácia de Monte Carlo (The Gambler’s Fallacy)
Também conhecida como a Falácia do Apostador, trata-se do viés cognitivo de acreditar que a frequência de curto prazo deve equilibrar a probabilidade de longo prazo. É a crença equivocada de que se o número 10 não é sorteado há 50 concursos, ele acumulou uma “energia” ou “dívida” estatística e terá mais chances de aparecer no próximo.
- A Realidade Matemática: O universo não possui um “registro de débitos”. Para o globo, não faz diferença se o número 10 saiu ontem ou há dez anos. A chance de ele sair hoje é exatamente a mesma de qualquer outra dezena.
- O Erro da Amostra: A Lei dos Grandes Números garante que, após milhões de sorteios, todos os números tenderão a ter saído o mesmo número de vezes. No entanto, com apenas cerca de 2.900 concursos realizados até 2025, a Mega-Sena ainda está no que chamamos de “ruído amostral”.
A Regressão à Média e o Ruído Estocástico
Muitos sistemas de predição tentam identificar “tendências” onde existem apenas flutuações aleatórias. Quando um número sai com muita frequência (os chamados “números quentes”), a estatística prevê uma Regressão à Média, mas ela não define quando isso ocorrerá. Tentar prever o próximo passo desse movimento é, por definição, impossível, pois o sistema carece de causalidade.
Caos Determinístico: O Fator Físico
Muitos acreditam que a imprevisibilidade da Mega-Sena reside apenas na estatística, mas o maior obstáculo à predição é, na verdade, físico. Embora o sorteio siga as leis da física clássica de Newton, ele se comporta como um Sistema Dinâmico Caótico.
O Determinismo Teórico vs. Prático
Em teoria, o sorteio é um evento determinístico. Se fôssemos capazes de mapear com precisão absoluta variáveis como:
- A massa exata de cada bola (até a escala de microgramas da tinta);
- A viscosidade e temperatura do ar dentro do globo;
- A velocidade angular do motor e a elasticidade das pás;
- O coeficiente de restituição (o “quique”) de cada colisão entre as bolas.
Poderíamos, através de equações de cinemática e dinâmica, calcular qual bola cairia no funil. É o que o físico Pierre-Simon Laplace chamaria de o “Demônio de Laplace”: uma inteligência que conhece todas as forças da natureza e poderia prever o futuro.
A Sensibilidade Extrema às Condições Iniciais (Efeito Borboleta)
O problema reside na sensibilidade extrema. Em sistemas caóticos, uma diferença ínfima nas condições iniciais é amplificada exponencialmente ao longo do tempo.
Uma variação de apenas 1 mícron (0,001 mm) na posição inicial de uma bola, ou uma flutuação de 0,1% na tensão elétrica que alimenta o motor do globo, altera completamente a trajetória das bolas após apenas alguns segundos de agitação. Esse fenômeno é o cerne da Teoria do Caos: o sistema é regido por leis fixas, mas o resultado final é indistinguível do acaso devido à impossibilidade de medição perfeita dos dados iniciais.
Colisões e Entropia Mecânica
Cada vez que uma bola colide com outra ou com a parede do globo, a incerteza sobre sua trajetória futura aumenta. Em um sorteio de aproximadamente 20 a 30 segundos, ocorrem milhares de micro-interações. Para um computador prever o resultado em tempo real, ele precisaria de um poder de processamento que superasse as flutuações atômicas do ambiente, o que torna a predição da Mega-Sena um problema computacionalmente intratável.
IA e Redes Neurais: Por que falham?
Com a ascensão de modelos de linguagem e redes neurais profundas, muitos entusiastas de tecnologia acreditam que basta “alimentar” um algoritmo com todos os resultados históricos da Mega-Sena para obter a combinação vencedora. Contudo, na arquitetura de dados, existe uma diferença fundamental entre reconhecimento de padrões e ruído aleatório.
Arquiteturas Sequenciais (LSTMs e Transformers)
Modelos como LSTM (Long Short-Term Memory) e Transformers (a base do ChatGPT) foram projetados para identificar dependências temporais em sequências de dados. No mercado financeiro, por exemplo, o preço de uma ação hoje tem correlação direta com o preço de ontem.
- O Problema da Entropia: Na Mega-Sena, a entropia é máxima. Não existe “memória do sistema”. Como cada sorteio é um evento de independência estatística, o modelo tenta encontrar uma função matemática que conecte o Concurso A ao Concurso B, mas essa função simplesmente não existe. A entrada de dados para a IA é, tecnicamente, ruído branco.
O Fenômeno do Overfitting (Sobreajuste)
O maior inimigo da predição de loterias via IA é o Overfitting. Ele ocorre quando o modelo de aprendizado de máquina se torna “especialista” demais nos dados de treinamento.
- A Ilusão da Regra: A rede neural pode identificar que, nos últimos 20 anos, sempre que o número 05 foi sorteado, o número 10 apareceu em 15% das vezes no concurso seguinte. O algoritmo “decora” essa correlação e a transforma em uma regra preditiva.
- A Realidade Estatística: Essa correlação é uma Coincidência Espúria. Em um universo de milhões de combinações, o acaso criará padrões temporários que parecem lógicos, mas não possuem causalidade. Quando o modelo é testado em dados novos (o próximo sorteio), a “regra” falha, pois ela foi baseada em ruído, não em um padrão sistêmico real.
Por que IAs são úteis, mas não preditivas?
Embora falhem em prever o número exato, as IAs são excelentes para realizar a filtragem negativa. Elas podem processar milhões de combinações e descartar aquelas que, embora possíveis, têm baixíssima probabilidade estatística de ocorrer (como sequências puramente lineares ou aglomerações em um único quadrante), ajudando o apostador a se manter dentro da “zona de normalidade” da Curva de Gauss.
A Impossibilidade Algorítmica: Por que o “Código” não pode ser Decifrado?
Frequentemente, desenvolvedores e entusiastas de dados tentam criar algoritmos de predição sob a premissa de que a Mega-Sena é um “quebra-cabeça” lógico. No entanto, a Teoria da Computação e a Entropia provam que o problema da predição de loterias é, por natureza, não-computável.
O Problema da Aleatoriedade Verdadeira (True Randomness)
A maioria dos algoritmos de computador gera números pseudoaleatórios, que dependem de uma semente (seed) inicial e um padrão lógico. Se a Mega-Sena fosse gerada por um software comum, ela seria previsível.
Contudo, o sorteio da Mega-Sena é um evento de aleatoriedade física real.
- A Barreira da Informação: Para que um algoritmo preveja o próximo concurso, ele precisaria de informações que não estão contidas no banco de dados de resultados passados. A “chave” para o próximo sorteio reside no estado microscópico da matéria dentro do globo no exato milésimo de segundo do sorteio, e não nos números que saíram há dez anos.
A Segunda Lei da Termodinâmica e a Entropia
A entropia é a medida da desordem de um sistema. Em um sorteio, a energia cinética fornecida pelo motor do globo é dissipada através de milhares de colisões aleatórias entre as bolas.
De acordo com a Segunda Lei da Termodinâmica, a desordem (entropia) de um sistema isolado tende a aumentar. Tentar prever a sequência sorteada seria o equivalente a tentar reverter a entropia: exigir que o algoritmo “organizasse” o caos físico em uma resposta lógica antes mesmo do evento ocorrer. Matematicamente, o esforço computacional necessário para simular todas as variáveis atômicas do globo superaria a capacidade de qualquer supercomputador atual.
A Falha da Regressão e do Reconhecimento de Padrões
Algoritmos de predição funcionam sob o princípio da indução: “se aconteceu muitas vezes no passado, acontecerá no futuro”.
- O Paradoxo do Ruído: Em ciência de dados, para que um padrão seja preditivo, ele deve ter correlação e causalidade. Na Mega-Sena, os dados históricos são o que chamamos de “ruído puro”. Qualquer algoritmo que tente encontrar uma função $f(x)$ que preveja o próximo sorteio acabará gerando uma resposta baseada em coincidências estatísticas que nunca se repetirão, um fenômeno técnico conhecido como Ilusão de Agrupamento.
Conclusão: O Papel da Estatística Otimizada
Se a matemática prova que é impossível prever o próximo sorteio, surge a pergunta inevitável: Para que serve a estatística na loteria? A resposta não está na “adivinhação”, mas na otimização de recursos. Em um jogo de chances ínfimas, a estatística atua como um filtro de eficiência, garantindo que o apostador não jogue contra si mesmo.
A Engenharia dos Desdobramentos (Wheeling Systems)
A estratégia de Wheeling é a aplicação prática da combinatória para cercar o prêmio. Em vez de depender de um único bilhete isolado, o apostador seleciona um conjunto maior de dezenas (ex: 9 ou 10 números) e utiliza um algoritmo para gerar combinações otimizadas entre elas.
- A Vantagem Matemática: O objetivo aqui não é prever a Sena, mas garantir matematicamente prêmios menores (Quadra ou Quina). Se o apostador acertar 4 das 9 dezenas escolhidas, o sistema de Wheeling garante que pelo menos um de seus bilhetes terá a Quadra, maximizando o retorno sobre o capital investido.
Entropia de Shannon e a Informação do Bilhete
Ao aplicar conceitos da Entropia de Shannon (Teoria da Informação), podemos medir o grau de “aleatoriedade útil” de uma aposta.
- Filtros de Improbabilidade: Jogar sequências como
01-02-03-04-05-06ou10-20-30-40-50-60possui uma entropia baixa. Embora tenham a mesma probabilidade teórica de qualquer outra combinação, elas pertencem a grupos de padrões que raramente se manifestam na realidade física dos sorteios. - Otimização: A estatística ajuda a selecionar jogos com alta entropia (distribuição caótica), que refletem fielmente o comportamento histórico dos globos de sorteio.
A Curva de Gauss como Bússola
A ferramenta mais poderosa do apostador estatístico é a Distribuição Normal. Ao analisar a soma das seis dezenas de todos os concursos anteriores, observamos uma concentração massiva no centro do espectro (geralmente entre 160 e 185).
Ao equilibrar suas dezenas para que a soma caia nessa “zona de calor”, o apostador não está prevendo o futuro, mas sim garantindo que sua aposta esteja dentro do território onde 40% a 50% de todos os sorteios da história já ocorreram. É a transição do “palpite cego” para a “aposta cientificamente fundamentada”.
Referências Bibliográficas
BARROSO, Nelson. A Matemática da Mega-Sena. Editora Ciência Moderna, 2021.
DATACAMP. Distribuição Gaussiana: o que é, propriedades e exemplos. DataCamp Tutorial, 2023. Disponível em: https://www.datacamp.com/pt/tutorial/gaussian-distribution. Acesso em: 21 dez. 2025.
FELLER, William. An Introduction to Probability Theory and Its Applications. Vol. 1. 3ª Edição. Wiley, 1968.
GLEICK, James. Caos: A Criação de uma Nova Ciência. Editora Campus, 1989.
GOODFELLOW, Ian; BENGIO, Yoshua; COURVILLE, Aaron. Deep Learning. MIT Press, 2016.
MOTT, Robert L.; UNTENER, Joseph A. Experiment 2: Bernoulli’s Theorem. Applied Fluid Mechanics. UTA Pressbooks, [s.d.]. Disponível em: https://uta.pressbooks.pub/appliedfluidmechanics/chapter/experiment-2/. Acesso em: 21 dez. 2025.
QUESTIONPRO. O que é a Função de Gauss e como ela funciona? QuestionPro Blog, 2023. Disponível em: https://www.questionpro.com/blog/pt-br/funcao-de-gauss/. Acesso em: 21 dez. 2025.
SHANNON, Claude E. A Mathematical Theory of Communication. Bell System Technical Journal, 1948.
3M SCIENCE AT HOME. Bernoulli Principle Experiment. 3M, [s.d.]. Disponível em: https://www.3m.com/3M/en_US/science-at-home-us/science-experiments-for-kids/bernoulli-principle-experiment/. Acesso em: 21 dez. 2025.
ZIBETTI, André W. Distribuição Normal. UFSC, [s.d.]. Disponível em: https://www.inf.ufsc.br/~andre.zibetti/probabilidade/normal.html. Acesso em: 21 dez. 2025.
BRASIL. Comissão de Valores Mobiliários (CVM). A falácia do jogador: uma análise psicológica das armadilhas mentais. Portal do Investidor, [s.d.]. Disponível em: https://www.gov.br/investidor/pt-br/penso-logo-invisto/a-falacia-do-jogador-uma-analise-psicologica-das-armadilhas-mentais. Acesso em: 21 dez. 2025.
Descubra mais sobre Régys Borges da Silveira
Assine para receber nossas notícias mais recentes por e-mail.
Dê-nos sua opinião, seu comentário ajuda o site a crescer e melhorar a qualidade dos artigos.